|
2. L’arrel digital d’un número
L'arrel digital d'un número és la que resulta de sumar
els seus dígits i, si aquesta suma és més gran o igual a 10, tornar a fer la
suma dels dígits d'aquesta suma i així successivament fins que s'obté un
nombre d'un dígit. Per exemple:
AD(1523)=AD(1+5+2+3)=AD(11)=2
AD(42513)=AD(4+2+5+1+3)=AD(15)=6
Feu un programa que escrigui l'arrel digital d'un número
natural. Podeu fer, tant una versió iterativa com una recursiva.
Anomeneu l'arxiu
font: m4e2.cpp
|
|
3.Càlcul de nombres combinatoris
Fent servir la funció factorial definida al resum teòric, construir una
funció que calculi el valor del nombre combinatori:
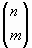
sabent que es calcula fent servir la fórmula:
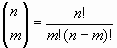
Aquest número representa el nombre de
combinacions diferents de m elements que es poden formar amb n elements.
Per exemple, amb 4 elements hi ha:
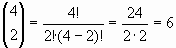
combinacions.
Si els 4 elements són {a,b,c,d}, aquestes 6 combinacions són:
{a,b} , {a,c} , {a,d} , {b,c} , {b,d} , {c,d}
Feu que el programa comprovi que n sigui més
gran o igual a m.
Anomeneu l'arxiu
font: m4e3.cpp
|
|
4. Successió de Fibonacci
Seguint les indicacions del resum teòric
respecte a la successió de Fibonacci, feu un programa que mostri els n
primers termes d'aquesta successió, essent n un nombre enter
entrat per teclat.
Anomeneu l'arxiu
font: m4e4.cpp
|
|
5.
Simulació del llançament de tres daus
Seguint l'esquema de la pràctica
6, feu una
simulació del llançament de tres daus 100.000 cops i verifiqueu d'aquesta
forma que la probabilitat de treure suma 9 i suma 10 és diferent. Només fa
falta que comptabilitzeu els cops que surt 9 i 10 i feu que surti per pantalla
les freqüències absolutes i relatives dels esdeveniments: suma 9 i suma 10.
Anomeneu l'arxiu
font: m4e5.cpp
|
|
Problemes
complementaris
Aquests exercicis serveixen per completar
aquest mòdul però suposen una ampliació voluntària. No és necessari
lliurar aquests exercicis. No obstant això, és convenient fer-los i
lliurar-los.
|
|
6.
Càlcul d'una àrea pel mètode d'acceptació-rebuig
Seguint les pautes de la pràctica
7 trobeu
l'àrea del recinte del quadrat de costat 2 que queda a sobre de la paràbola y
= x2.
El dibuix de l'àrea que es vol calcular és la
part ombrejada del dibuix adjunt. Els vèrtexs del rectangle són (-1, 0),
(-1,1), (1,1) i (1, 0).
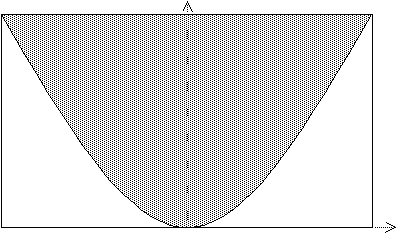
El procés ha de consistir en generar punts del
rectangle, és a dir, parells de nombres aleatoris:
- x, un nombre aleatori entre -1 i 1 (exactament
igual que a la pràctica 7)
- y, un nombre aleatori entre 0 i 1.
Els punts de la zona d'acceptació compleixen
que y>x2.
Podeu comprovar el resultat obtingut amb el
valor exacte d'aquesta àrea que és 4/3.
Anomeneu l'arxiu
font: m4e6.cpp
|
|
7.
Nombres combinatoris (II)
A l'exercici 3 s'ha proposat un programa que
contingui una funció que calculi un número combinatori fent servir la
funció factorial. En molts casos, el càlcul d'un número combinatori es pot
simplificar si en lloc de fer servir la fórmula:
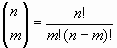
utilitzem aquesta altra equivalent:
La raó és que n! pot ser molt més
gran que el numerador de la fórmula anterior i, per aquest motiu, es pot
produir un error d'overflow o sobrecàrrega, a més que el temps en
el càlcul de la segona fórmula és més petit.
Feu un programa que implementi la funció combinatori de la segona forma i compareu els resultats amb la funció de
l'exercici 3 amb números combinatoris com:
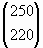
Anomeneu l'arxiu
font: m4e7.cpp
|
|
8.
Nombres combinatoris (III)
Encara hi ha una altra forma
d'implementar el càlcul dels nombres combinatoris, es tracta de fer servir la
relació:
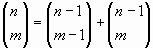
Per tant, es pot definir una funció
recursiva en la qual, els casos de sortida siguin:
Si n=m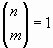 
i si m=0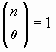 
Implementeu aquesta funció. Anomeneu l'arxiu font: m4e8.cpp
|
 |
 |
