|
3. Lleis de Morgan
Les
lleis de Morgan permeten relacionar els connectors lògics "i" i
"o". Aquestes lleis són: no
(p i
q) º no
p o no
q no (p
o q) º
(no p) i (no q) on
p i q són expressions lògiques. Per tal de comprovar aquestes lleis fareu
servir els operadors lògics de C/C++: !
, && i || Heu
de calcular per als quatre casos possibles de valors de p i q les
expressions lògiques: !(p||q)
!p&&!q
per tal de comprovar la primera llei i: !(p&&q)
!p||!q
per tal de comprovar la segona llei. En
lloc dels valors numèrics 1 i 0, definiu les macros V i F tal i com s'ha
fet a la pràctica 4.
Anomeneu al programa m2e3.cpp i feu-lo
dintre d'un projecte anomenat m2e3 a l'espai de treball m2.
Heu d'enviar només l'arxiu:
m2e3.cpp. No envieu l'arxiu executable.
|
|
4.
Verificació de condicions amb operadors relacionals
Seguint la mateixa pauta que a la
pràctica 6,
feu un programa que demani les coordenades del centre d'una circumferència (a,b),
el seu radi r i les coordenades d'un altre punt (x,y). El
programa ha d'escriure un 1 si el punt (x,y) pertany al cercle definit
per la circumferència {(a,b), r }, en cas contrari ha d'escriure un 0.
No s'ha de fer servir cap sentència if, només heu d'emprar operadors
aritmètics, relacionals i lògics.
Es recorda que la condició que el punt (x,y)
pertanyi al cercle de centre (a,b) i radi r és:
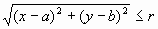 o
bé o
bé
(x - a)2 + (y -
b)2 <= r2
és a dir, que la distància del punt (x,y)
al punt (a,b) sigui més petita o igual al radi.
Per aquest programa feu que totes les variables
siguin del tipus double.
Anomeneu al programa m2e4.cpp i feu-lo
dintre d'un projecte anomenat m2e4 a l'espai de treball m2.
Heu d'enviar només l'arxiu:
m2e4.cpp. No envieu l'arxiu executable.
|
|
5. Localització
d'una cel·la
Un rectangle està dividida en n
files i m columnes. Les files estan numerades des del 0 fins al n-1
i les columnes des del 0 fins al m-1. Es tracta d'escriure un programa que, donat
un número p comprés entre 0 i nxm-1, ens indiqui a
quina fila i columna pertany aquest número. Per exemple, si el rectangle
està dividit en n = 4 files i m = 5 columnes i escrivim p
= 14, ha de
respondre: fila 2, columna 4.
|
col
0 |
col
1 |
col
2 |
col
3 |
col
4 |
| fila
0 |
0 |
1 |
2 |
3 |
4 |
| fila
1 |
5 |
6 |
7 |
8 |
9 |
| fila
2 |
10 |
11 |
12 |
13 |
14 |
| fila
3 |
15 |
16 |
17 |
18 |
19 |
El programa haurà de demanar els valors de n,
m i p, tots enters.
Com a pista direm que si els
números de la primera fila els dividim per n (5 en aquest cas)
el quocient té part entera igual a 0, és a dir, la fila a la qual pertanyen.
I el mateix passa amb totes les files
Anomeneu al programa m2e5.cpp i feu-lo
dintre d'un projecte anomenat m2e5 a l'espai de treball m2.
Heu d'enviar només l'arxiu:
m2e5.cpp. No envieu l'arxiu executable.
|
|
6. Paràmetres
estadístics amb tres dades
En aquest exercici es tracta de fer un programa
que calculi la mitjana aritmètica, la mitjana geomètrica, la variança i la
desviació típica d'un conjunt de tres dades del tipus double, per
això, heu de crear tres funcions amb els següents protocols:
double mitjaa(double,double,double);
//mitjana aritmètica
double mitjag(double,double,double);
//mitjana geomètrica
double var(double,double,double);
//variança
|
La primera funció retornarà el valor de la
mitjana aritmètica dels tres números, és a dir, la suma dividit per 3.
La segona funció retornarà el valor de la
mitjana geomètrica dels tres números, és a dir, l'arrel cúbica del
producte dels tres. Per tal de fer l'arrel cúbica heu de fer servir la
funció pow() on el segon argument haurà de ser 1./3 (Atenció!!, 1/3 no
és el mateix que 1./3):

La tercera funció retornarà la variança dels tres números. La variança
de tres números: a,b,c, es pot calcular com la mitjana aritmètica
dels quadrats d'a,b i c menys el quadrat de la mitjana aritmètica d'a,b
i c, és a dir:
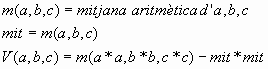
Per últim, per tal de calcular la desviació
típica de les dades només s'ha de recordar que la desviació típica és
l'arrel quadrada de la variança.
Per poder fer servir les funcions
matemàtiques: pow() i sqrt() és necessari incloure l'arxiu
capçalera math.h.
Anomeneu al programa m2e6.cpp i feu-lo
dintre d'un projecte anomenat m2e6 a l'espai de treball m2.
Heu d'enviar només l'arxiu:
m2e6.cpp. No envieu l'arxiu executable.
|
|
Exercicis
complementaris
Aquests exercicis serveixen per completar
aquest mòdul però suposen una ampliació voluntària. No és necessari
lliurar aquests exercicis. No obstant això, és convenient fer-los i
lliurar-los.
7. La descomposició horària
Escriviu un programa que llegeixi un nombre
natural que representa un cert temps en segons (per exemple: 125342 segons)
i escrigui la seva descomposició en dies, hores, minuts i segons (per
exemple: 1 dies, 10 hores, 49 minuts, 2 segons).
Anomeneu al programa m2e7.cpp i feu-lo
dintre d'un projecte anomenat m2e7 a l'espai de treball m2.
|
|
8. Àrea
d'un triangle
Feu un programa que, donats els tres punts,
escrigui l'àrea del triangle que formen.
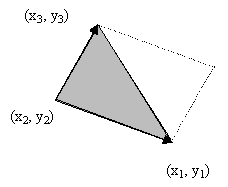
Si els vèrtexs introduïts
són (x1, y1), (x2, y2) i (x3,
y3), l'àrea del paral·lelogram determinat per aquests
punts coincideix amb el mòdul del producte vectorial dels vectors:
u = (x1-x2
, y1-y2 , 0) i v = (x3-x2 , y3-y2,
0)
és a dir:
A=|(x1-x2)(y3-y2)-(y1-y2)(x3-x2)|
i, per tant, l'àrea del triangle serà:
A=0.5·|(x1-x2)(y3-y2)-(y1-y2)(x3-x2)|
Per aquest programa feu que totes les variables
siguin del tipus double.
Anomeneu al programa m2e8.cpp i feu-lo
dintre d'un projecte anomenat m2e8 a l'espai de treball m2.
|
 |
 |